Рассмотрено Срочно

[hermaeus mora.]

1) Ваш ник: mu ha
2) Дата и время выдачи наказания: -
3) Ник администратора: vse
4) Суть жалобы: помогите интегралы развязать, а то мама компьютер заберет и не смогу играть на дрп
5) Обязательно скриншот/видео (... с вмешательством или сделанные от другого лица будут отклоняться!):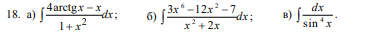

6) Ваш Discord/VK (не обязательный пункт): можете сюда ответы давать

 

[hermaeus mora.]

@Leonardo Kingsman Вы как гений математики тоже можете помочь

 

[polyasha ♡︎]

Приветствую.
Возможно, будут ошибки, ибо интегралы проходили стопицот лет назад.
Первый интеграл. дробим на два с одинаковым знаменателем - 4arcrgx/1+x^2 и -x/1+x^. Когда дробите, не забывайте про минус!!!
4 выносим, а arctgx преобразуем в t. Получится 4 * ∫ tdt. По свойству получаем 4 * t^2/2. Делаем обратную замену: 4 * arctg (x)^2/2. Упрощаем: 2arctg(x)^2.
Вторая часть интеграла ну очень изи. Опять же, делаем подстановку, t = 1+x^2. Получаем интеграл -∫1/2t dt. 1/2 выносим за знак интеграла: - 1/2∫1/t dt. Получается -1/2 ln|t|. Делаем обратную замену: -1/2 ln |1+x^2|.
Фигачим все вместе и получаем: 2arctgx^2 - 1/2 ln(1+x^2) + c.

Второооой интеграл. Тут банально, от ответа страшно. Опять же метод замены переменной.
Для начала разберемся с числителем: разделим числитель на знаменатель, т.к. числитель должен иметь меньшую степень.
Получим: 3x^4 - 6x^3 + 12x^2 - 24x + 36 + (-72x-7)/(x^2+2x). Далее проводим махинации по упрощению и выносу общего х, получим: 3x^4 - 6x^3 + 12x^2 - 24x + 36 - 7/2x - 137/2(x+2)
Подставляем интегралы. Далее более - менее табличные. Получим:
3x^5/5 - 3x^4/2 + 4x^3 + 36x - 7/2 ln|x| - 137 ln|x+2|
И не забываем про константу в конце.

Третий интеграл хорошо расписан в этом видеоролике. ​

 

[William Hennet]

 

[hermaeus mora.]

Посмотреть вложение 1975413

не работает чета

 

[Demetrio Medina]

У меня катка в доте нашлась, напишите в вк: vk.com/axel6932, помогу после нее.

 

[❤ Frank Linton ❤]

Я умный по-сути, и...

Приветствую.
Возможно, будут ошибки, ибо интегралы проходили стопицот лет назад.
Первый интеграл. дробим на два с одинаковым знаменателем - 4arcrgx/1+x^2 и -x/1+x^. Когда дробите, не забывайте про минус!!!
4 выносим, а arctgx преобразуем в t. Получится 4 * ∫ tdt. По свойству получаем 4 * t^2/2. Делаем обратную замену: 4 * arctg (x)^2/2. Упрощаем: 2arctg(x)^2.
Вторая часть интеграла ну очень изи. Опять же, делаем подстановку, t = 1+x^2. Получаем интеграл -∫1/2t dt. 1/2 выносим за знак интеграла: - 1/2∫1/t dt. Получается -1/2 ln|t|. Делаем обратную замену: -1/2 ln |1+x^2|.
Фигачим все вместе и получаем: 2arctgx^2 - 1/2 ln(1+x^2) + c.

Второооой интеграл. Тут банально, от ответа страшно. Опять же метод замены переменной.
Для начала разберемся с числителем: разделим числитель на знаменатель, т.к. числитель должен иметь меньшую степень.
Получим: 3x^4 - 6x^3 + 12x^2 - 24x + 36 + (-72x-7)/(x^2+2x). Далее проводим махинации по упрощению и выносу общего х, получим: 3x^4 - 6x^3 + 12x^2 - 24x + 36 - 7/2x - 137/2(x+2)
Подставляем интегралы. Далее более - менее табличные. Получим:
3x^5/5 - 3x^4/2 + 4x^3 + 36x - 7/2 ln|x| - 137 ln|x+2|
И не забываем про константу в конце.

Третий интеграл хорошо расписан в этом видеоролике. ​

Тут всё правильно. Согласен.

 

[hermaeus mora.]

+рэп девочке дайте кабанчиком в виде ликесов
и повысьте

согласен с нечаевом, очень сильно помогла. Можете закрывать

 

[Roberto Reddington]

Приветствую.
Возможно, будут ошибки, ибо интегралы проходили стопицот лет назад.
Первый интеграл. дробим на два с одинаковым знаменателем - 4arcrgx/1+x^2 и -x/1+x^. Когда дробите, не забывайте про минус!!!
4 выносим, а arctgx преобразуем в t. Получится 4 * ∫ tdt. По свойству получаем 4 * t^2/2. Делаем обратную замену: 4 * arctg (x)^2/2. Упрощаем: 2arctg(x)^2.
Вторая часть интеграла ну очень изи. Опять же, делаем подстановку, t = 1+x^2. Получаем интеграл -∫1/2t dt. 1/2 выносим за знак интеграла: - 1/2∫1/t dt. Получается -1/2 ln|t|. Делаем обратную замену: -1/2 ln |1+x^2|.
Фигачим все вместе и получаем: 2arctgx^2 - 1/2 ln(1+x^2) + c.

Второооой интеграл. Тут банально, от ответа страшно. Опять же метод замены переменной.
Для начала разберемся с числителем: разделим числитель на знаменатель, т.к. числитель должен иметь меньшую степень.
Получим: 3x^4 - 6x^3 + 12x^2 - 24x + 36 + (-72x-7)/(x^2+2x). Далее проводим махинации по упрощению и выносу общего х, получим: 3x^4 - 6x^3 + 12x^2 - 24x + 36 - 7/2x - 137/2(x+2)
Подставляем интегралы. Далее более - менее табличные. Получим:
3x^5/5 - 3x^4/2 + 4x^3 + 36x - 7/2 ln|x| - 137 ln|x+2|
И не забываем про константу в конце.

Третий интеграл хорошо расписан в этом видеоролике. ​

Не девушка, а мечта

 

[matthew lessard.]

Приветствую.
Помогли.
Закрыто.